Robustness | Cross-Domain Ensembles

Overview Video

An overview video (12 mins) explaining our method is given below. Please turn on your speaker for narration.

Quick Summary

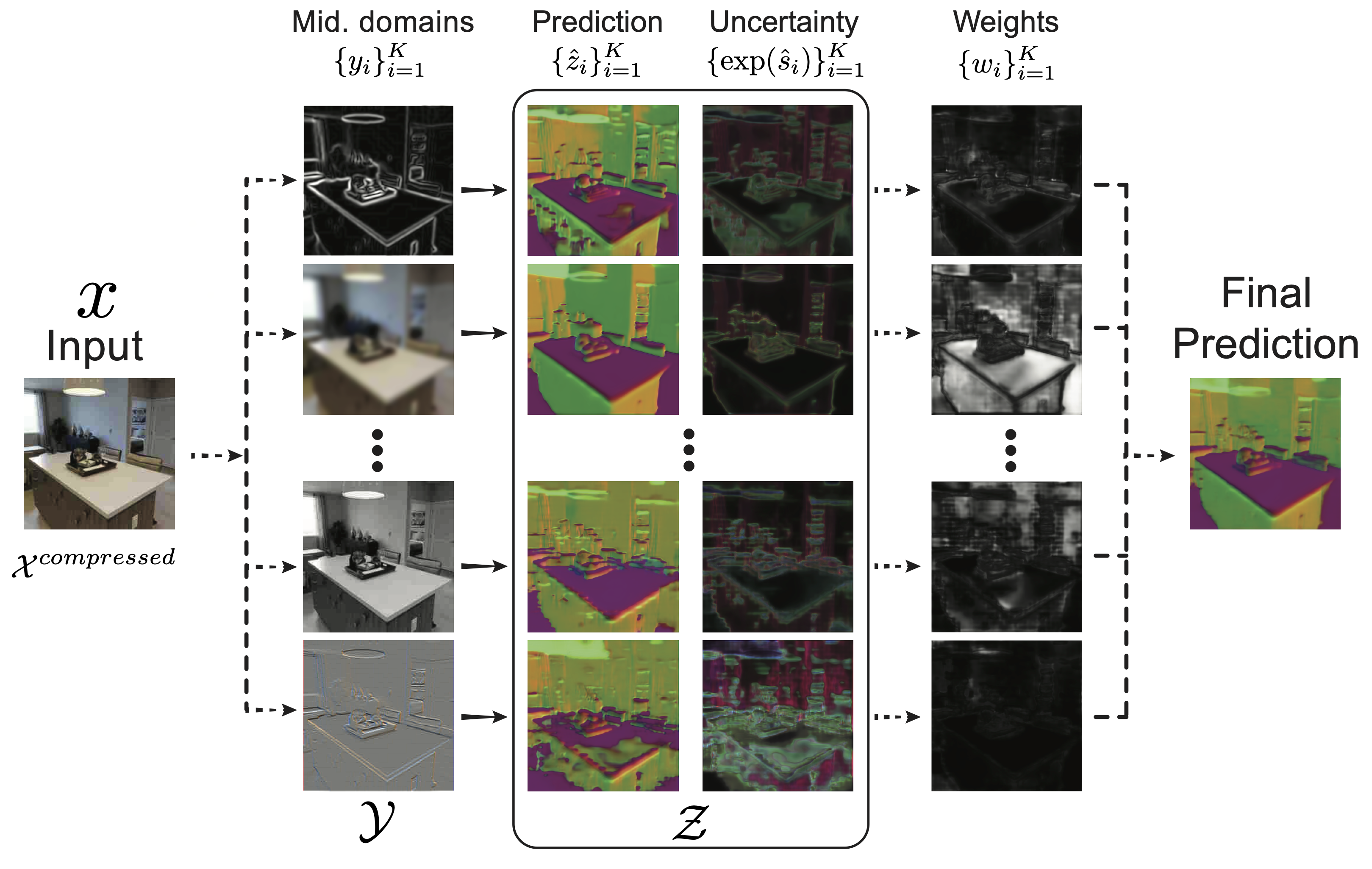
An overview of our method for creating an ensemble of diverse prediction paths. A network is trained to go from an input that has undergone an unknown distribution shift (e.g. JPEG compression degradation) to a target domain, e.g. surface normals, via several middle domains, e.g. 2D texture edges, low-pass filtering, greyscale, emboss filtering, etc. We then compute the corresponding weights of these predictions based on their uncertainties. The final prediction is obtained by a weighted average. Solid arrows represent learned mappings and dashed ones represent analytical mappings.

Robustness Of Neural Networks

Neural networks deployed in the real-world will encounter data with naturally occurring distortions, e.g. motion blur, brightness changes, etc. Such changes make up shifts from the training data distribution. While neural networks are able to learn complex functions in-distribution, their predictions are deemed unreliable under such shifts, i.e. they are not robust. This presents a core challenge that needs to be solved for these models to be reliable in the real-world.

The video below shows the predictions of standard methods against our proposed approach applied frame by frame on a query YouTube video. Our predictions are notably more resistant to natural distortions that occur across video frames.

(Note: Videos on page best seen in HD)

How Do We Obtain Robust Predictions?

Suppose we want to learn a mapping from an input domain, e.g. RGB images, to a target domain, e.g. surface normals (see Figure above). A common approach is learning a direct path, i.e. RGB→surface normals. Since it directly operates on the input domain, it is prone to being affected by any slight alterations in the RGB image, e.g. brightness changes. An alternative can be to go through a middle domain that is invariant to that change. For example, the surface normals predicted via the RGB→2D edges→surface normals path will be resilient to brightness changes in the input as the 2D edges domain abstracts those away. However, the distortions that a model can encounter are broad and unknown ahead of time, and some middle domains can be too lossy. These can be mitigated by employing an ensemble of predictions made via a diverse set of middle domains and merging their predictions into one strong output on-the-fly.

We first select a set of middle domains from which we learn to predict the final domain. Each path reacts differently to a particular distribution shift, so its prediction may or may not degrade. We also estimate the uncertainty of the each path's prediction, which allows us to employ a principled way of combining them. Prior knowledge of the relationship between middle domains is not needed as their contribution to the final prediction are guided by their predicted uncertainties. The middle domains we adopt are all self-supervised (they can be programmatically extracted), thus, this framework does not require any additional supervision/labeling than what the dataset comes with. We show that the method performs well, insensitive to the choice of middle domains and it generalizes to completely novel non-adversarial and adversarial corruptions.

The Method In Action

The following figure demonstrates this with a concrete example. For a given image, each path's prediction, uncertainty, and corresponding weights are shown. For the pixelated image in the left, each path reacted differently to the distortion, and the final prediction is obtained by combining individual predictions based on their uncertainties. Similar observations can be made for the glass blurred image in the right, where the method learned weights in a way such that the degraded paths are not used in the final prediction.

The quality of the final prediction depends on the following elements:

• For each pixel, at least one middle domain is robust against the encountered distortion,
• The uncertainty estimates are well correlated with error, allowing the merger to select regions from the best performing path. Uniform merging does not take into account the uncertainties and consequently lead to worse predictions.

How does it work? Each network in each path receives different cues for making a prediction, due to going through different middle domains. Left: Given a distorted pixelated query, each path (columns) is affected differently by the distortion, which is reflected in its prediction, uncertainty, and weights (lighter means higher weights/uncertainty). The inverse variance merging uses the weights to assemble the final prediction that is better than each of the individual predictions. Right: Similarly, for a query with glass blur distortion, the method successfully disregards the degraded predictions and assembles an accurate final prediction. Note that the proposed method (inverse variance merging) obtains significantly better results than learning from the RGB directly (leftmost column of each example) which is the most common approach. The elliptical markers denotes sample regions where the merged result is better than all individual predictions.

Below we show how this works on a video. See how each path contributes to the final prediction based on its uncertainty.

Addressing Overconfident Inaccurate Predictions

As shown above, our method uses uncertainty estimates to merge the predictions from each path. However, uncertainty estimates under distribution shifts are poorly calibrated, i.e. there is a tendency to output a poor prediction with high confidence. Below we describe how we can overcome this with an additional training step.

We propose a calibration step, denoted as sigma training to encourage the network to output high uncertainties while keeping predictions fixed. The video at the right shows the predictions and uncertainties before and after this step on an image corrupted with increasing distortion. Before sigma training, when the model produces poor results, its uncertainty does not increase correpondingly. After sigma training, the uncertainty estimates have a stronger correlation with error.

Sample Results

Some qualitative results on videos and image queries are shown below. The former are on external YouTube videos and the predictions are made frame-by-frame with no temporal smoothing. Zoom in to see the fine-grained details. See the paper for full details.

Key takeaways:

• Using middle domains I. promotes ensemble diversity, which improves performances by decorrelating errors, II. reduces the tendency of individual networks to learn from superficial cues. The uncertainty based merging allows the method to select regions from the best performing path. This allows us to attain:
• Robustness against natural distortions: We compare against several baselines and show that our method is robust to a wide range of natural distortions. In particular, we compare against adversarial training which is a popular way of making networks robust and show that it does not lead to robustness against natural distortions.
• Robustness against adversarial attacks: The method is also shown to be more robust to attacks compared to baselines without adversarial training.
• Robustness on classification tasks: The improved performance on ImageNet and CIFAR confirms the basic value of using middle domains.
• Furthermore, improvements in robustness does not sacrifice performance on in-distribution data and has a negligible increase in computational cost compared to standard ensembles.

Results on pixel-wise prediction tasks

The query video below has been corrupted by increasing shot noise and pixelation. Our method returns more accurate predictions with less flickering.

The predictions below for the different target domains further demonstrates the generalizability of our method.

Qualitative results under synthetic and natural distribution shifts for normal, reshading, and depth. The first four rows show the predictions from a query image from the Taskonomy test set under no distortion and increasing speckle noise. Our method degrades less than the other baselines, demonstrating the effectiveness of using different cues to obtain a robust prediction. The last three rows shows the results from external queries. Our method demonstrates better generalization to images considerably different from the training dataset.

Improvements are further supported by quantitative results. The l1 error over a wide range of distortions are lower for the proposed approach (inv. var. merging) compared to the baselines in all three target domains and shift intensities.

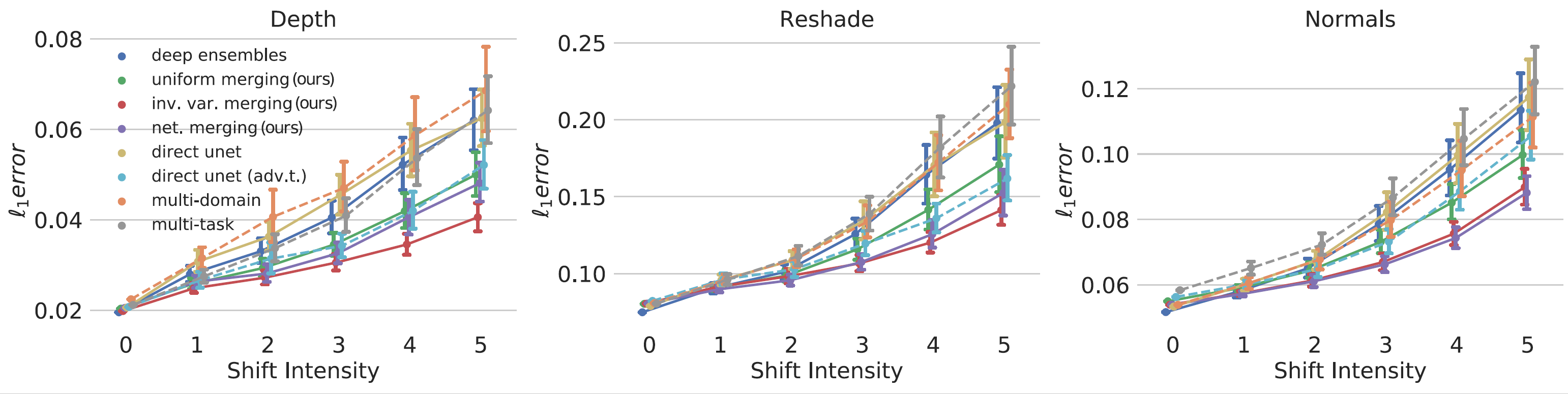
Quantitative results: Average l1 loss over 11 unseen distortions from Common Corruptions. Error bars correspond to the bootstrapped standard error. Our proposed approach is more robust against distribution shifts.

Generalization of sigmas to distribution shifts:

We have showed that our method returns predictions that are robust under a wide range of distribution shifts. Are our predicted uncertainties also able to generalize under distribution shifts, i.e. do we get high uncertainties when predictions get worse? To investigate this, we consider epistemic uncertainty which is used to capture the model's uncertainty and is an indicator of distribution shifts.
The video at the right shows the predictions and epistemic uncertainties on an image corrupted with increasing distortion. Deep ensembles produce overconfident uncertainties under distortion, while our method shows an increasing trend.

Results on adversarial attacks

The video below compares our method and the baselines under attacks generated by the I-FGSM under increasing values of epsilon. Neither our method nor the baselines utilize explicit adversarial defense mechanisms -- while deep ensembles performs nearly as poorly as baseline UNet, the proposed method performs significantly better. This indicates that using middle domains promotes ensemble diversity in a way that makes it more challenging to create an attack that fools all paths simultaneously. The analytical operations to attain the middle domains are deterministic and differentiable, i.e. we do not obfuscate gradients. See the paper for more details and further results.

Results on classification task

The proposed method is not limited to regression tasks. The video below shows the performance on ImageNet under increasing distortion and clean inputs. Our method performs noticeably better compared to baselines by only averaging predictions from a diverse set of middle domains. See the paper for more details and additional results.